生存分析——KM曲线

Ziyu
Date : September 25, 2023
Categories : 生信工具
Tags : 拷贝数变异

罗列生存分析中最常用的2个绘图方法：

KM曲线
cox分析

以下内容主要来源于《医学统计学基础》姜晶梅主编，在此基础上按照自己的理解习惯稍作修改。

1. 概念引入

在研究中，观察结果在短期内不确定，研究者不仅关心事件的发生与否（比如肿瘤是否转移），还关心事件发生所经历的时间，同时考虑“事件”和“时间”。另外还存在失访从而无法获得事件发生的准确时间。

起始事件（initial event）：标志研究对象生存过程开始的事件，比如疾病确诊或首次用药。根据研究目标确定。
终点事件（endpoint event/failure event）：研究对象的特定结局，比如肿瘤转移。根据研究目标确定。
生存时间（survival time/failure time）：从起始事件到终点事件所经历的时间称为生存时间。
完全数据（complete data）：终点事件发生在研究结束前，并且能够得到准确的生存时间称为完全数据。
删失数据（censored data/incomplete data）：由于各种原因未能观察到研究对象的终点事件，从而无法获知研究对象的准确生存时间，称之为“删失”。删失分为左删失和右删失两种情况，右删失指在终点事件发生在最后一次随访时间的右方，个体的真实生存时间长于观察到的生存时间，左删失指的是个体的生存时间短于观察到的生存时间。

删除的原因主要有三种：

失访（loss to follow-up）：失去联系（研究对象主动退出，无应答等等）或者由于其他原因死亡而未观察到规定的终点事件。
患者的生存时间超过了预先设定的研究终止期。
动物实验中，有时预先规定多少个动物发生了终点事件就中止实验，实验停止时，有一部分动物没有出现终点事件，也属于删失数据。

生存时间是一个随机变量（常用$ T $表示），常用的统计量：

概率密度函数：生存时间是随机变量，因此有相应的概率分布。假定生存时间T服从含有未知参数的某种分布，概率密度函数表示为：

$f (t) = lim_{△ t \to 0} \frac{P {t \leq T < t + △ t}}{△ t}$ $= lim_{△ t \to 0} \frac{P {个体在 [t, t + △ t) 内发生终点事件}}{△ t}$

$ \bigtriangleup t $是指一段非常小的时间区间，生存时间的概率密度函数表示在某时刻t终点事件发生的瞬时速率。

生存函数：概率密度函数$ f(t) $的累积形式称为生存函数（survival function），也称累积生存概率或生存率。生存函数用$ S(t) $表示，是指个体生存时间$ T $大于t的可能性，表达式为：

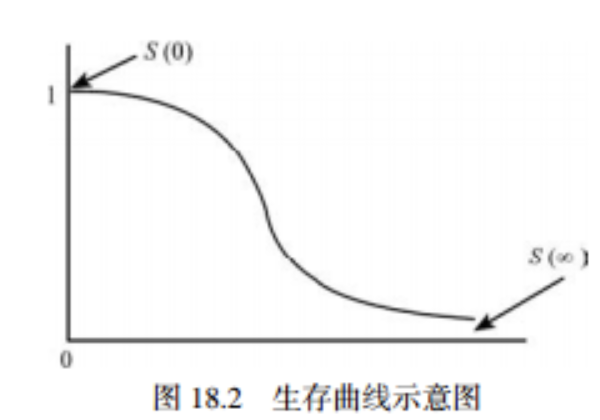
$ S(t) $是对生存过程的描述，表示没有发生终点事件的累积概率，该函数随着时间t而减小，$ S(0)=1 $，$ S(\infty)=0 $

实际计算时一般如下估计：

$$ S(t)=\frac{生存时间T>t的个体数}{随访个体总数} $$

生存曲线：以生存时间t为横轴，以$ S(t) $为纵轴，讲各个时间点所对应的生存率连接在一起绘制成的曲线为生存曲线。理论上，生存曲线是一条平滑曲线，由于实际数据分析中常采用非参数方法估计生存率，所以生存曲线多呈现阶梯形状。

风险函数（hazard function）：指研究对象活过t时刻后，在t到$ t + \bigtriangleup t $这一段很短时间内终点事件发生概率和$ \bigtriangleup t $之比的极限值，一般用$ h(t) $表示。计算公式为：

$h (t) = lim_{△ t \to 0} \frac{P {t \leq T <（ t + △ t ） | T \geq t}}{△ t}$

含义为生存时间已达t的个体，在t时刻发生终点事件的瞬时风险率，反应的是速率变化的快慢而不是概率值，因此风险函数又称为条件死亡率，瞬时死亡率等等。

生存函数是对生存过程的描述，表示没有发生终点事件的累积概率，与生存函数所呈现的信息相反，风险函数$ h(t) $表示了终点事件发生的瞬时风险，通常反映某疾病对生命的影响过程，$ h(t) $的取值范围是$ [0,\infty) $，实际计算时，$ h(t) $如下估计：

$$ h(t)=\frac{在[t,t+\bigtriangleup t)内发生终点事件的个体数}{在t时刻尚存活的个体数\times \bigtriangleup t} $$

$ h(t) $可以是常量或者增函数、减函数等等。常见的$ h(t) $如下所示：

【图片】

$ S(t) $，$ f(t) $和$ h(t) $是紧密相连的，对$ h(t) $进行数学变换：

2. 生存率的估计

为了了解生存资料的特征，在获得生存数据后首先对其进行描述性分析，包括参数方法和非参数方法。参数方法可以借助现有的理论分布来描述样本生存时间，如指数分布、Weibull分布、Gamma分布、对数正态分布、线性指数分布和Gompertz分布等。但由于随访资料中生存时间的分布难以确定，并经常存在删失数据，限制了参数方法在实践中的应用。非参数方法在生存资料的描述中更方便实用。

2.1 乘法极限法（KM曲线）

乘积极限法是针对随机删失数据估计生存函数的非参数方法，又称为Kaplan-Meier method（KM），可用于右删失数据的处理，主要应用于小样本未分组资料，也可以用于大样本生存数据。

乘积极限法的基本原理是利用条件概率的乘法原理来估计生存率，假设将终点事件发生的时间按照从小到大排序$ t_{1} < …< t_{D} $，$ Y_{i} $表示$ t_{i} $时刻刚开始的个体数，$ d_{i} $表示$ t_{i} $时刻发生的终点事件数，$ d_{i}/Y_{i} $是条件概率的估计值，即生存时间恰好达到$ t_{i} $时刻的个体在$ t_{i} $时刻发生终点事件的条件概率，则KM估计量计算公式为：

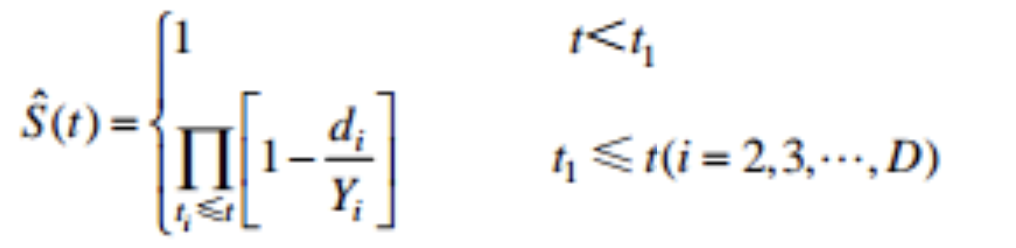
KM估计量是一个阶梯函数，终点事件发生的时间点处是其跳跃间断点，以上计算的样本生存率是总体生存率的点估计值，生存率的（1-a）x100%置信区间计算公式为：

示例数据

mdat <- matrix(
  c(
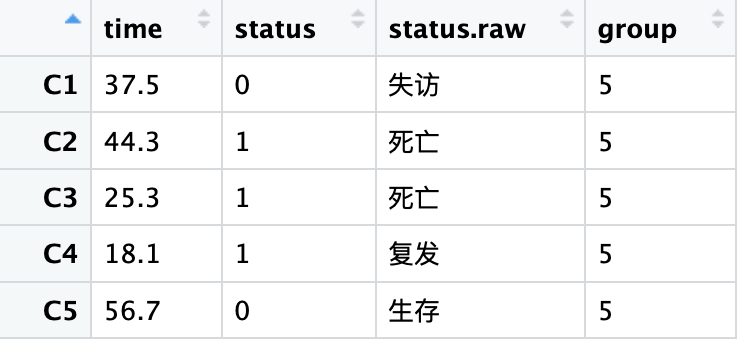
    37.5,0,"失访",5,
    44.3,1,"死亡",5,
    25.3,1,"死亡",5,
    18.1,1,"复发",5,
    56.7,0,"生存",5
    ), 
  nrow = 5, 
  ncol = 4, 
  byrow = TRUE,
  dimnames = list(
    c("C1", "C2", "C3","C4","C5"),
    c("time", "status","status.raw","group"))) %>%
  as.data.frame()

km_fit <- survfit(Surv(time, status)~group, data = mdat)

km_fit %>%ggsurvplot(data = mdat,
                     fun = "pct",
                     risk.table = TRUE,
                     fontsize = 3, # used in risk table
                     surv.median.line = "hv", # median horizontal and vertical ref lines
                     ggtheme = theme_light(),
                     # title = "Kaplan-Meier Survival Function Estimate",
                     legend.title = "",
                     # legend.labs = levels(mdat$group)
)

对于生存资料，应用图形展示生存过程会更加直观。示例的计算结果以生存时间为横坐标，生存率为纵坐标绘制生存曲线：

根据公式计算生存率和标准误：

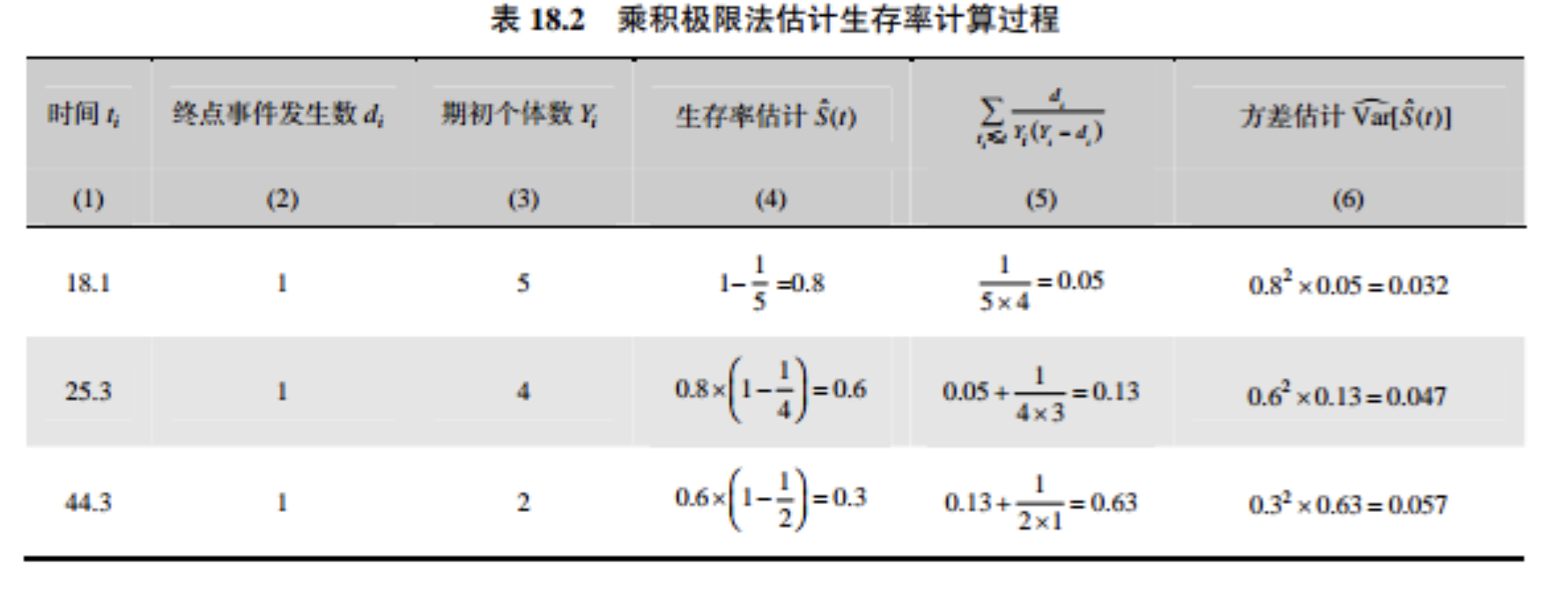
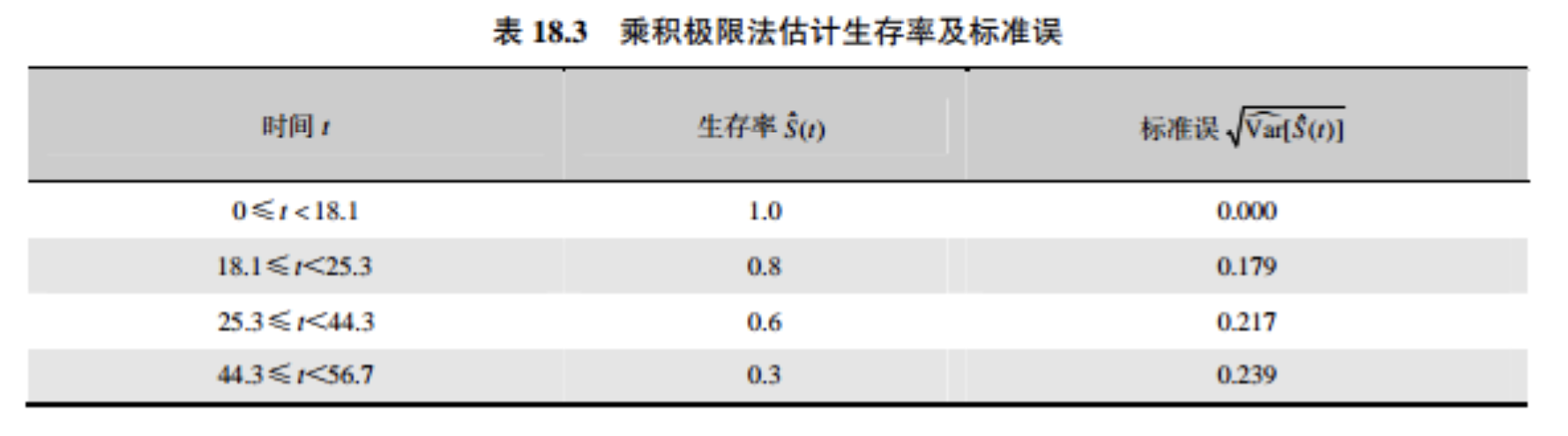
生存曲线的每一级阶梯代表一个终点事件发生的时间点，图中的三个阶梯依次代表了4、3和2号患者的死亡/复发事件，阶梯对应的横坐标为终点事件发生的时间点。在删失时间点无阶梯，圆圈依次表示1号和5号患者删失，其对应的横坐标为删失时间点。由于本例数据中最大的生存时间点是删失数据，因此生存曲线不与横轴相交，否则生存曲线在生存时间点处与横轴相交。由于随着观察时间的增加，观察例数越来越少，一般曲线尾部显示的生存率可能不稳定。

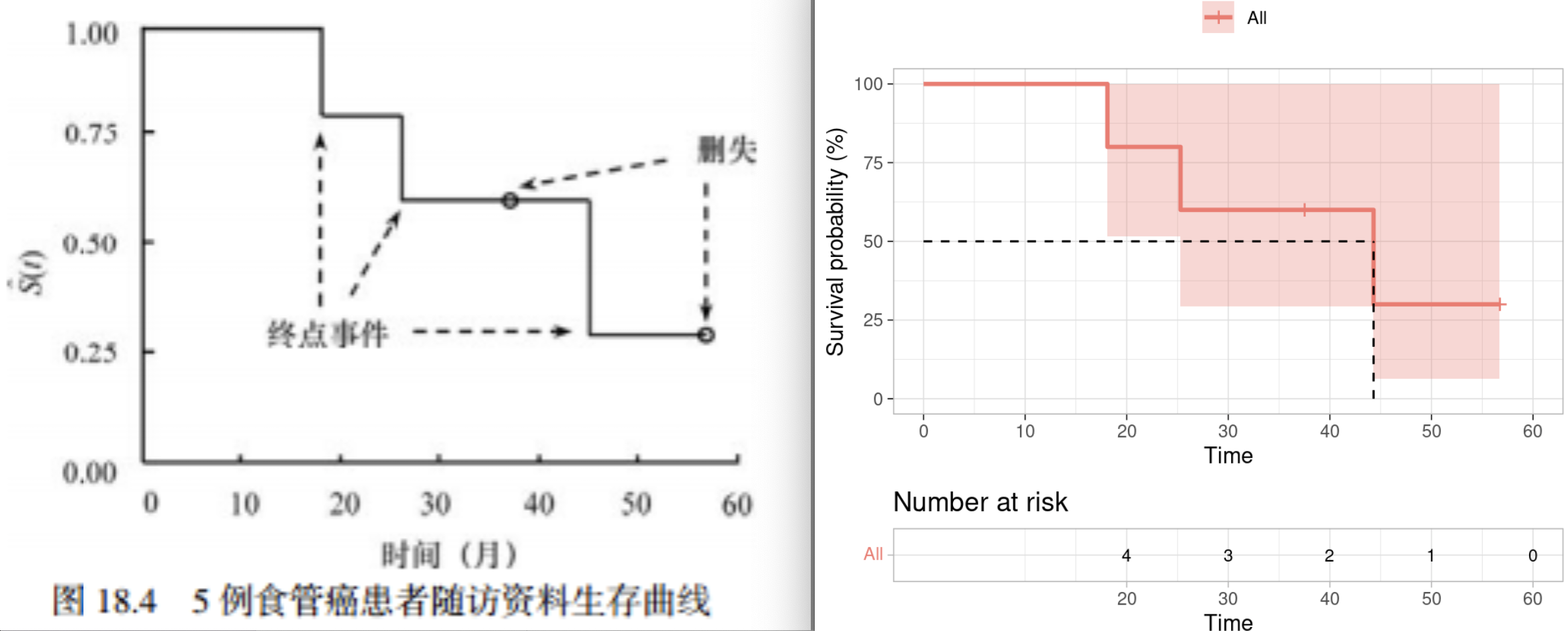
注意一下这里的risk table里面，样本数对应的位置是（未删失+未发生事件）的样本数【这个画图的结果没有从5开始，有点奇怪】。

2.2 寿命表法

样本量较大的时候【这里的样本量多大的时候需要用寿命表法呢，不手动计算生存率的情况下还有必要去使用寿命表法吗】，可以将生存时间的观察值范围划分为若干小区间，采用寿命表法（life-table method）计算生存函数。区间的划分方法不同，寿命表的计算结果也不同，一般情况下使用较小的时间单位准确性更高。

乘法极限法与寿命表法本质相同，都是通过一系列条件概率的乘积来计算生存概率，二者的区别在于寿命表法是在小区间上估计条件概率，称发际线法是将观察到的时间点作为小区间的极限。

3. 生存过程的比较

实践中经常会对两个或多个生存曲线进行比较，由于抽样误差的影响，还需要对其进行假设检验，检验方法有很多种，以下主要介绍常用的时序检验法（log-rank test）。

3.1 时序检验

该检验属于非参数方法，比较的是整个生存时间的分布（整条生存曲线），并不是比较某个时间点上的生存率。时序检验的原假设H0：两条生存曲线相同，备择假设H1：两条生存曲线不同。时序检验的本质是大样本$ X_{2} $检验，基本思想是：计算不同时间点上两组的期初观察人数及终点事件发生人数，并在H0条件下分别计算出两组在该时间点的期望终点事件发生人数，实际值与期望值一旦相差过大，则有理由认为这个差异不仅仅由抽样误差造成，即两个总体生存曲线有统计学差异。

除了时序检验以外，还有Wilcoxon检验、Tarone-Ware检验、Peto检验等，他们的区别在于各时间点上终点事件发生数实际值和期望值的差赋予的权重不同。以两组生存曲线比较为例，检验统计量的一般形式：

上述这些方法都属于单因素分析，考虑多种预后因素的影响需要借助多因素分析方法，比如cox回归模型。

参考资料

封面from hiplot